| СОДЕРЖАНИЕ | СЛЕДУЮЩИЙ РАЗДЕЛ |
Тема 4.5 Зубчатые передачи
Цилиндрическая косозубая зубчатая передача
4.5.2 Эквивалентное колесо
4.5.3 Силы в зацеплении
4.5.4 Расчет на контактную прочность 4.5.5 Расчёт зубьев на изгиб
В результате изучения студент должен знать:
4.5.1 Геометрия и кинематика косозубых цилиндрических передач
- геометрические параметры цилиндрической косозубой передачи;
- формулы для расчета сил в зацеплении;
- формулы для расчета косозубых передач на контактную прочность и изгиб.
Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение рис. 2.3.14.
;
Рис. 2.3.1 Цилиндрическая косозубая а) и шевронная б) передача
С увеличением угла наклона
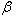линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются рис.2.3.15, но при этом увеличивается и осевая сила Fа, что нежелательно. Поэтому в косозубых передачах принимают угол 
.
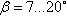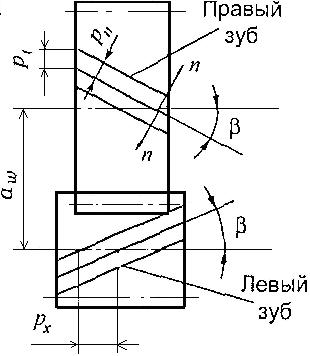
Рисунок 2.3.15 Геометрия косозубых колес
нормальный шаг зубьев pn - в нормальном сечении,
окружной шаг pt – в торцовом сечении; при этом
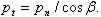
Соответственно шагам имеем два модуля зубьев:
(2.3.22)
(2.3.23)при этом
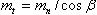(2.3.24)где mt и mn – окружной и нормальный модули зубьев.
За расчётный принимают модуль mn, значение которого должно соответствовать стандартному. Это объясняется следующим: для нарезания косых зубьев используется тот же инструмент, что и для прямозубых, но с соответствующим поворотом инструмента относительно заготовки на угол
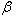. Поэтому профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба; следовательно, mn=m.Диаметры делительный и начальный
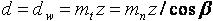(2.3.25)
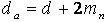(2.3.26)
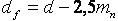(2.3.27)
(2.3.28)4.5.2 Эквивалентное колесо
Профиль косого колеса в нормальном сечении n-n (рис. 3) соответствует исходному контуру инструментальной рейки и, следовательно, совпадает с профилем прямозубого колеса.
Расчет косозубых колес проводят через параметры эквивалентного прямозубого колеса. Нормальное к линии зуба сечение делительного цилиндра имеет форму эллипса. Радиус кривизны эллипса при зацеплении зубьев в полюсе 
профиль зуба в этом сечении достаточно близко совпадает с профилем приведённого прямозубого колеса, называемого эквивалентным,профиль зуба в этом сечении достаточно близко совпадает с профилем приведённого прямозубого колеса, называемого эквивалентным.
Делительный диаметр: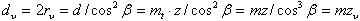 
(2.3.29)
эквивалентное число зубьев: 
(2.3.30)
или 
(2.3.31)
где z – действительное число зубьев косозубого колеса.
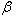
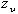
С увеличением возрастает возрастает 
. Это одна из причин повышения прочности косозубых передач.
4.5.3 Силы в зацеплении
Силы в зацеплении определяют в полюсе зацепления. Сила 
, действующая на зуб косозубого колеса рис. 2.3.16, направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса и составляет угол 
с касательной к эллипсу.
Рисунок 2.3.16Схема действия сил в зацеплении косозубых колесРазложим эту силу на две составляющие: окружную силу на эквивалентном колесе:
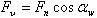(2.3.22) радиальную силу на этом колесе:
(2.3.33)Переходя от эквивалентного к косозубому колесу, заметим, что сила
является радиальной силой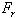 
и для этого колеса, т.е.
сила Ft расположена в плоскости, касательной к начальному цилиндру, и составляет угол
с осью колеса. Разложим силу Ft на две составляющие:окружную силу
(2.3.35),и осевую силу
(2.3.36).Окружная сила известна. Её определяют по передаваемому моменту и диаметру делительной окружности зубчатого колеса
(2.3.37)Тогда из формулы (2.3.35):
следует 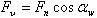Подставив силу и выражения , окончательно получим:радиальную силу
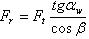(2.3.38) и осевую силу
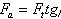(2.3.39).На зубья шестерни и колеса действуют одинаковые, но противоположно направленные силы. При определении их направления учитывают направление вращения колёс и направление наклона линии зубьев
(правое и левое). Наличие в зацеплении осевой силы, которая дополнительно нагружает валы и подшипники, является недостатком косозубых передач.
4.5.4. Расчет на контактную прочность
Вследствие наклона зубьев в зацеплении одновременно находится несколько пар зубьев, что уменьшает нагрузку на один зуб, повышая его прочность (снижая расчётные напряжения).
Аналогично расчету прямозубой передачи межосевое расстояние для косозубых колес определяют по формуле (2.3.17):
,где Ка = 43 МПа – для косозубых колес.
Контактные напряжения в поверхностном слое зубьев
,где
- коэффициент нагрузки при расчете по контактным напряжениям;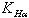
- 1,04 – 1,13 коэффициент нагрузки, учитывающий распределение нагрузки между зубьями и зависит от окружной скорости; 
- коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий); для косозубых передач выбирается с учетом расположения колеса на валу и термообработки;
- коэффициент нагрузки, учитывающий дополнительные динамические нагрузки =1,02-1,06 при любой твердости, скорость до 10 м/с, =1,1 при твердости поверхности не больше 350 НВ и скорости 10-20 м/с, =1,05 при твердости более 350 НВ и скорости 10-20 м/с.Косозубые передачи работают более плавно, чем прямозубые, поэтому коэффициент
, меньше. Условие контактной прочности косозубой передачи
,Если условие не выполняется, то изменяют ширину венца колеса b2, не выходя за пределы рекомендуемых значений
. Если это не даст желательного результата, то либо назначает другие материалы колёс или другую термообработку, и расчёт повторяют.Расчет допускаемых напряжений ведется аналогично расчету прямозубых колес
4.5.5 Расчёт зубьев на изгиб
Наклонное расположение зубьев увеличивает их прочность на изгиб и уменьшает динамические нагрузки. Это учитывается введением в расчётную формулу прямозубых передач поправочных коэффициентов 
и 
.
Формула проверочного расчёта косозубых передач
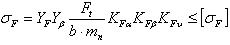(2.3.41),где YF - коэффициент формы зуба выбирают по эквивалентному числу зубьев zv;
- коэффициент, учитывающий наклон зуба;
- коэффициент распределения нагрузки по ширине венца определяют по аналогии с прямозубыми передачами;
= 0,81-0,91 - коэффициент распределения нагрузки между зубьями;
- коэффициент нагрузки, учитывающий дополнительные динамические нагрузки
=1,2 при твердости зубьев не больше 350НВ,
= 1,1 при твердости зубьев более 350 НВ.
Нормальный модуль зубьев mn определяют по аналогии с прямозубыми передачами. При некоторых средних значениях коэффициентов получим формулу для приближенного определения модуля косозубых передач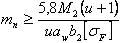
(2.3.42),и для шевронных передач
(2.3.43),При проверке по формуле (2.3.41):
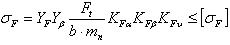можно получить 
значительно меньше 
, что не является недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб.Если расчётное значение превышает допускаемое, то применяют колёса, нарезанные с положительным смещением инструмента, или увеличивают m; > означает, что в передаче из данных материалов решающее значение имеет не контактная прочность, а прочность зубьев на изгиб. На практике к таким передачам относятся передачи с высокой твёрдостью рабочих поверхностей зубьев – 51…63HRCэ (цементация, нитроцементация, азотирование). Проектировочный расчёт таких передач следует выполнять с целью обеспечения прочности зубьев на изгиб по форме определения минимально допустимого модуля m, а затем выполнить проверочный расчёт зубьев на контактную прочность.
Ответьте на контрольные вопросы
| СОДЕРЖАНИЕ | СЛЕДУЮЩИЙ РАЗДЕЛ |
